| | LA PARADOJA
1 = 0.999... |
“La identidad 0.999... = 1 es una convención” (Timothy Gowers)
“0.999… no representa un número, sino un proceso” (The Straight Dope)
“El argumento que finalmente me convenció fue el siguiente: deben ser iguales [1 y 0.999...] porque no hay hueco para encajar ningún otro decimal entre ellos” (Steven Strogatz)
La Paradoja
Se admite en matemática que 1 = 0.999... (abreviadamente, 0,9). La paradoja consiste en: ¿Cómo es posible que un mismo número tenga dos expresiones distintas en el mismo sistema de numeración (el de base 10)? ¿Cómo es posible que un número finito (1) sea igual a un número expresado con infinitas cifras decimales (0.999...)?
Hay muchos argumentos o demostraciones a favor de esta igualdad:
- Puesto que 1/3 = 0.333..., multiplicando por 3 ambos lados de la igualdad, se tiene: 1 = 0.999...
Análogamente, Puesto que 1/9 = 0.111..., multiplicando por 9 ambos lados de la igualdad, se tiene: 1 = 0.999...
- Si x = 0.999... y 1 fueran distintos, existiría un número intermedio entre ambos, lo que parece que no es el caso, pues (1 + x)/2 = 1.999.../2 = 0.999... = x
- Si x = 0.999..., entonces multiplicando por 10 ambos términos, tenemos:
10x = 9.999... (se desplaza el punto decimal una posición a la derecha)
Pero 9.999... = 9 + 0.999... = 9 + x
Por lo tanto, 10x = 9+x y x=1.
- Un número decimal periódico puro no es más que una forma disfrazada de una serie aritmética infinita. Si tenemos la progresión aritmética a, ar, ar2, ar3,..., con r<1, su suma es x = a+ar+ar2+ar3+... Multiplicando ambos lados por r, tenemos:
xr = ar + ar2 + ar3 +... = x−a
x=a/(1−r)
El número 0.999... es la suma de los elementos de la progresión geométrica infinita 0.9, 0.09, 0.009, …, cuya razón es 0.1 y cuya suma es 0.9/(1 − 0.1) = 1.
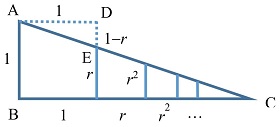
- Existe también una demostración geométrica debida a Benjamin G. Klein e Irl C. Bivens [1988]:
En la figura, el triángulo ABC es semejante al triángulo ADE. Por lo tanto, x/1 = 1/(1 − r), siendo
Esto es fácilmente generalizable a
x = a + ar + ar2 + ar3 +…
La expresión 0.999... = 1 es generalizable. Todo número decimal finito tiene un gemelo con infinitos nueves. Ejemplos:
2 = 1.999…
0.25 = 0.24999…
28.327 = 28.326999…
La paradoja ...999 = −1
Esta paradoja se ha presentado como la dual de la anterior.
Si sumamos 1 a y = ...999, el resultado es cero: y+1 = 0. Por lo tanto, y = −1.
Si tenemos x = 0.999... 10x = x+9 x=1, entonces tenemos análogamente:
y = ...999 y/10 = y + 0.9 y = −1.
Se ve que x e y son opuestos entre sí: su suma es cero: x+y = 0.
Se produce la paradoja de que un número infinitamente grande (...999) es igual a −1, y que 0.999... y ...999 son opuestos entre sí: 0.999... = −...999
Este resultado se puede generalizar para cualquier secuencia de dígitos que se repitan indefinidamente. Por ejemplo,
x = 0.341341341...
103x = x+341
x = 341/(103−1)
y = ...341341341
y/103 = y + 0.341
y = −341/(103−1)
Las fórmulas generales para una secuencia m de longitud n son:
x = m/(10n−1)
y = −m/(10n−1)
Todos los números compuestos de infinitas secuencias de dígitos caen entre −1 y +1.
Los números del tipo x+y son siempre cero, independientemente de la secuencia de dígitos. Por ejemplo, ...341341341.341341341… = 0
Explicación de las paradojas
Los números 1/3 y 1/9 son inexpresables de manera exacta y finita en el sistema de numeración de base 10 porque 3 y 9 no son submúltiplos de 10, siendo 0.333... y 0.111... las máximas aproximaciones posibles, respectivamente. En cambio, en base 3 estos números se expresan de manera exacta y finita: 1/3 = 0.1(3 y 1/9 = 0.01(3.
0.999… no es un número concreto, sino un número frontera entre lo finito y lo infinito. Está infinitamente próximo a 1 y se expresa con infinitas cifras decimales. Es un número que podemos calificar como imaginario porque implica el infinito. El número 0.999... y todos los que tienen infinitas cifras decimales se pueden calificar de “imaginarios”.
La expresión 1 – 0.999... es un infinitésimo, un número infinitamente próximo a cero, pero no es cero. Un infinitésimo es un número real positivo y menor que cualquier número real positivo. Este número no existe, es imaginario. Como 1 – 0.999… es un infinitésimo, 1 – 0.999... > 0 y 1 > 0.999...
La expresión 1 = 0.999... es una expresión que implica la conciencia porque conecta los dos modos de conciencia, une los opuestos: lo finito y lo infinito, lo cuantitativo y lo cualitativo, lo operativo y lo descriptivo, lo real y lo imaginario, lo racional y lo intuitivo.
Por lo tanto, 0.999... no es 1. Y ...999 no es −1. En el caso de 0.999... se trata de la suma de infinitos sumandos cuyo límite es 1. La igualdad 0.999... = 1 es un convenio basado en la noción de límite: el valor de una serie infinita que tiene como límite un valor finito es el valor de su límite.
La Representación de Cantor
Cantor [1869] inventó un sistema que permite representar cualquier número racional de forma exacta mediante una secuencia finita. Con este sistema las fracciones se pueden representar sin pérdida alguna de precisión [Wayner, 1988].
En el sistema de Cantor se utiliza una base factorial: cada valor de posición es igual al factorial de dicha posición:
...(5!)(4!)(3!)(2!)(1!).(1/2!)(1/3!)(1/4!)(1/5!)...
es decir,
...(120)(24)(6)(2)(1).(1/2)(1/6)(1/24)(1/120)...
Por ejemplo,
301.102(F = 3*3! + 0*2! + 1*1! + 1/2! + 1/3! + 2/4!
en donde el subíndice F indica “base factorial”.
Se puede demostrar que un número anan−1...a1.a1a2...an(F basado en factoriales cumple la propiedad 0 ≤ ai ≤ |i|, es decir, el número que tiene los dígitos máximos es
...5 4 3 2 1.1 2 3 4 5...
Propiedades
- 1·1! + 2·2! + ... + n·n! = (n+1)! – 1
Por ejamplo: 1·1! + 2·2! + 3·3! + 4·4! = 5! – 1
- 1/2! + 2/3! + 3/4! + ...`+ (n−1) = 1 − 1/n!
Por ejemplo,
1/2! + 2/3! + 3/4! = 1 − 1/4!
Estas propiedades permiten establecer analogías entre el sistema basado en factoriales y el sistema exponencial tradicional de base 10. Por ejemplo:
| Exponencial | Factorial
|
| 999 = 1000 − 1 | 321(F = 1000(F − 1
|
| 0.999 = 1 − 0.001 | 0.123(F = 1 − 0.001(F
|
Ejemplos de representación de números enteros
| Número | Representación
|
| 1 | 1(F
|
| 2 | 10(F
|
| 3 | 11(F
|
| 4 | 20(F
|
| 5 | 21(F
|
| 6 | 100(F
|
| 7 | 101(F
|
| 8 | 110(F
|
| 9 | 111(F
|
| 10 | 120(F
|
Ejemplos de representación de fracciones menores que 1
| Fracción | Representación
|
| 1/2 = 1/2! | 0.1(F
|
| 1/3 = 2/3! | 0.02(F
|
| 2/3 = 1/2! + 1/3! | 0.11(F
|
| 1/4 = 1/3! + 2/4! | 0.012(F
|
| 3/4 = 1/2! + 1/3! + 2/4! | 0.112(F
|
| 1/5 = 1/3! + 1/4! + 2/5! | 0.0104(F
|
El número e
Como curiosidad hay que decir que el número e se representa como
10.111...(F = 10.1(F puesto que
e = ∑(1/i!) (sumatoria entre 0 e infinito)
Los factoriales como “anti-primos”
Así como los números primos hacen referencia a sí mismos y representan arquetipos matemáticos, los factoriales constituyen el polo opuesto a los primos −podemos denominarlos “anti-primos”− son las máximas manifestaciones superficiales porque contienen como factores a una serie de números consecutivos a partir del 1, que son todos sus divisores. El factorial de un número n contiene (aritméticamente hablando) a los números 1 a n, es decir, n! puede dividirse en grupos iguales de 1 (n grupos), 2 (n/2 grupos), 3 (n/3 grupos), ..., n (1 grupo).
Por lo tanto, representar los números con el sistema de Cantor tiene dos ventajas fundamentales:
- Se fundamenta o apoya en los números de máximo nivel de manifestación.
- Los números racionales se representan de forma finita y sin pérdida de precisión. No hay casos en los que aparezcan infinitas cifras decimales, como con la representación tradicional.
Bibliografía
- Cantor, George. Über Die Einfachen Zahlensysteme. Zeitschrift für Mathmatik und Physik, vol, 14, 1869, pp. 121-128.
- Dauben, Joseph Warren. George Cantor. His Mathematics and Philosophy of the Infinite. Princeton University Press, 1990.
- Gazale, Midhat. Number. From Ahmes to Cantor. Princeton University Press, 2000.
- Klein, Benjamin G.; Bivens, Irl C. Proof without words. Mathematics Magazine, 61 (4), October 1988.
- Strogatz, Steven. El placer de la X. Taurus, 2013.
- Wayner, Peter. Error-Free Fractions. BYTE, Junio 1988, pp. 289-298.